"Abstract Comics and Systems Theory," talk given at the San Diego Comic Arts Conference, 2011

(Note: this is a paper I delivered in July 2011 at the Comic Art Conference, the annual academic meeting of comics scholars held in conjunction with the San Diego Comic-Con, in a session organized by Matt Smith and Randy Duncan.  I've been meaning for a while to expand it and publish it, but as 2012 turns into 2013, I'm realizing that I've sat on these ideas for long enough and that I should get them out there sooner rather than later; so I will post it here for now as delivered, and hopefully start a conversation in view of a future expansion.  Please note the qualifications and excuses in the opening paragraph of the talk.  Calling my approach "impressionistic" still strikes me as right, even though I believe that each point could be defended at much greater length with reference to specific texts.  That being the case, please try to read the essay"poetically" if nothing else, listening for the--possibly only metaphorical--parallel between science and the comics genre to which this blog is devoted.

One more thing:  a full bibliography would be longer, but here were the main books that were on my desk as I wrote this, and from which I scanned all the images below that come neither from comics nor from Google Earth:  Ian Stewart, Does God Play Dice: The Mathematics of Chaos,1990;  Ian Stewart and Martin Golubitsky, Fearful Symmetry: Is God a Geometer?, 1992; James Gleick, Chaos: Making a New Science, 1987; Ilya Prigogine and Isabelle Stengers, Order out of Chaos: Man's New Dialogue with Nature, 1984; Hermann Weyl, Symmetry, 1952; Ludwig von Betalanffy, General Systems Theory, 1969; Andrew Hodges, Alan Turing: The Enigma, 1983; Edward N. Lorenz, The Essence of Chaos, 1995.

Oh, and now you can see. I hope, why I chose to preface this post by posting the entirety of The World is An Abstract Comic three days ago. The illustrations below are taken from the Powerpoint slides I used in my talk.)

When I gave Randy and Matt the topic for this talk, I did not realize that, in researching it, it would become quite as complex as it since has. In order to fulfill the promise of the abstract, I fear, this talk would need to be twice as long. However, only to treat a small part of it might not convey the full significance of the issue. Therefore this talk will end up being less detailed than I would have liked it to be. It deals with a number of related notions connected to the scientific—physical or chemical, and even sociological—concept of “system”; yet I will need to treat these subjects rather impressionistically. For example, when using a notion such as that of vector field, I will not have the time to give the specific mathematical definition of it, but I trust that the notion of a--in our case--two dimensional field structured by directional vectors should be at least intuitively clear.

It is appropriate that I am discussing this subject here in Southern California. I first began to consider it in the Spring of 2008 when I found myself flying repeatedly from my home in Indiana to Los Angeles.
At the time I was in the process of putting together my anthology, Abstract Comics, and therefore I had on my mind a number of configurations of how comics function abstractly--non-representationally and non-narratively--as for example in these, two of my favorite examples from the book, the work of Gary Panter and Benoit Joly.

At the same time I was working on my own comics; as a matter of fact, I had recently completed a series titled “24 x 24: A Vague Epic,” of which these are two pages.

So, as I was flying back and forth from Indy to LA with abstract comics on my mind, I had an experience which many of you may have had too—that is, to look down at the ground and admire the sheer abstract beauty of the landscape far below me. You may have seen many times before aerial photographs that look like abstract paintings—or at least that we can appreciate as such since the advent of abstract art itself (not to mention of airflight):

New artistic forms introduce new ways of aesthetic perception into the world. We then can apply these new ways to the appreciation of things outside of the strict artistic realm, which then become accidental artworks, in a sense. Of course, as I was thinking not simply of abstract painting, but of abstract comics at the time, I found myself noticing rectangular suburban subdivisions or farming plots dedicated to different crops, and realizing to what extent they seemed to be structured in patterns very much like a comic. I didn’t have a camera on me, so later I found myself going on Google Earth to find some of the same configurations. Of course, I wasn’t able to find the exact same parcels of land, but here is an example, from about where I first had this thought, under what I guessed was my flight path into LA.

You can see a structured field, and what, in this context, may look like panels and panels within panels, the specific texture and color of which is defined by the respective composition of the soil and the cultivated crop, the habitation, the presence or absence of larger vegetation such as trees; while the panel structure itself is imposed by the man-made network of roads and paths and real-estate lots. It’s a formality of structure, which obviously is not intentionally sequential, but which strangely has some of the same systematic arrangement as rectangular panels within the larger rectangle of a comic page.

That summer I found myself doing this repeatedly, and coming up with a short series of “found art” which I called “The World is An Abstract Comic.” Here are two more examples.

On the left you see a portion of Mississauga, Ontario, re-colored but with its original structure left intact; you can see not only an arrangement into “panels,” but even a larger, winding avenue—connecting neighborhoods to each other, cutting through the planned grid—that provides us with a parallel to the familiar trajectory of comics reading, from top right to bottom left. On the right, a portion of Queensland, Australia, which, if you look at it aesthetically, so to speak, seems to have the subtle tones and pictorial effects of a painted page by Bill Sienkiewicz or Dave McKean.

 What we see here is that, within a specific grid system, imposed by humankind, due to a variety of factors--geographic, meteorological, geological, but also sociological and political--a differentiation of the grid takes place, leading to an emergent organization that is more complex than either the simple notion of the idealized grid, or for that matter than the earth would have looked had a grid system not been imposed on it. The grid provides a structure within which differentiation can occur, and homogeneity fades away in a process of--let me introduce here this important notion--symmetry breaking. In the words of Ian Stewart and Martin Golubitsky, this phenomenon “occurs when a symmetric [or homogenous] system starts to behave less symmetrically. In some manner… symmetry gets lost.”

Symmetry-breaking is perhaps the most important process for pattern formation in the natural world, and it leads to increased complexity. The notion, first seriously studied by Alan Turing in 1952, has been taken up by numerous disciplines recently, to the extent to which even cosmologists see the formation of the universe as the ultimate example of the creation of a complex system via the breaking of symmetry. Returning back to earth, as it were, in our examples the modular sameness of the ideal grid gives way, differentiating the “panels” both in texture and also in structure, form, orientation; and the simple homogeneity of the pre-existing natural world is broken itself, inasmuch as differing crops are isolated from each other, in a kind of agricultural analogy to Maxwell’s demon.

These aerial views, as I already mentioned, suggested to me an analogy to the basic functioning of a comic: to begin with, the grids of farm plots or city blocks visible in them are comparable to another idealized grid, the one that underlies our experience of any comic. I say idealized because the potential for the subdivision of the page into panels, and of the distribution of narrative moments across those panels, precedes any actual act of comic making, any specific choice of breakdown or layout. Furthermore, they pointed to the equally basic fact that, before you can have sequence, you need differentiation; in order to have a comic at all, the panels need to be different from each other. While this similarity--between the gridded earth surface and the panel grid--may seem accidental, keep in mind that, even in such plots of land, the structuring is due to a human activity of shaping and forming. In this structuring imposed by human action onto the natural world--world which, in its turn, proceeds to differentiate itself within the superimposed grid--we can begin noticing elements of cross-influence and formal conflict that lead to contrast between “panels,” to arising opposite vectors of force, etc. This structure is NOT fundamentally different from how a complex comic functions formally, and indeed, I would argue, it seems to be echoed in the structure, and process of structuring, of the abstract comics page--or of any comics page, in general.

There is a more obvious way in which natural, physical phenomena can be structured by human activity to seem to echo, or be echoed by, abstract comics. For example, visual records of various scientific processes are usually arranged for publication in sequential art form (the main difference seeming to be that, for some reason, the conventions of scientific illustration require columns to be read first from top to bottom, and then the eye to move to the next column, rather than going first across then down):

Now these are clearly time based sequences, paralleled, for example, by the apparent "moment-to-moment"  morphing of quasi-biological forms in Lewis Trondheim's Bleu, or in many other metamorphosis-based abstract comics:

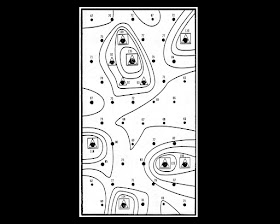
The examples could be multiplied at leisure, but let me just give you one more example of such a process, which also happens to chronicle an increase of geographical complexity from a basic grid system via symmetry-breaking. Here is a classic computer model of urbanization. You have to imagine an earlier panel, not shown, in which we have a simple grid of localities, each with an equal number of inhabitants—67—and with no extended spheres of influence, as marked by the curved lines here. Now, after a number of possible determinants have been input, we see the development of urban centers due to commerce, economic forces, and so on:

We also see power being centered in some areas which extend their influence over other localities, their population increasing while in other places the population stagnates or even decreases. Of course it is a computer model, situated within an idealized, flat topography. Had it been applied to a real-world area, the final result would, on a much larger scale, have been similar to the Google-Earth based images I showed you earlier. We see in this model transformation from a purely homogenous space to an articulated space through differentiation and symmetry breaking, and we can easily picture how any similar real-world areas came to be formed.

As is typical with systems theory, which finds similar patterns across widely divergent fields of research, the development of complexity in the urbanization model strangely parallels Alan Turing’s first studies of symmetry breaking, from 1952, on the chemical basis of morphogenesis—form creation, or what we can think here of as the development of complexity in a biological organism. Turing did an early modeling of pattern formation on animal hides, and here is a later elaboration of the same model by Jim Murray (also in the form of a comic!):

Most importantly for us, Turing speculated that symmetry breaking occurs within a morphogenetic field—a preexisting “field” of information (in the case of the embryo, Turing speculated it was a varied chemical field) that helps translate genetic information to transform the homogenous embryonic blastula, or blob of cells, into an organism with front-back, left-right, and top-bottom differentiation.

While biologists came to reject the notion of a chemical morphogenetic field in favor of a purely gene-based development (though it has recently been re-introduced by evolutionary biologist Rupert Sheldrake), Turing’s modeling has remained important for the study of any number of system developments.

Looking back to the urbanization model, the development of it reveals the vectors of force inherent in the functioning of such a field: essentially, the grid of localities is charged by any number of economic, political, etc., forces and interactions, tensions which undermine the stability of the primordial grid and allow it to differentiate into complexity. The variation from first to last stage, as seen here, shows how the differentiation process occurred, but the field itself is also plainly visible in the variation of forces, intensities, in the last stage itself.

I hope you can see the same underlying field of tensions as having created any of the topography-based “found abstract comics” I showed you earlier. I would argue that it is by perceiving formally that underlying field of tensions, with its resultant forces and transformations, that we are led to appreciate aesthetically—with the aesthetics of an abstract comic, really—found artworks of this kind. I know I’m running out of time so, for the sake of brevity, let me state my thesis succinctly at this point: abstract comics can model complex systems. Within the idealized, pre-existing grid, the formation of a comic necessarily involves differentiation and symmetry breaking. And finally, this happens because any comic has a pre-existing morphogenetic field: that is, the potential panel grid, turned into a vector field by the presupposed top-to-bottom, left-to-right direction of reading, together with the differentiation expected between any two panels if sequentiality is to occur.

To stay within my time limit, I will at this point skip illustrating this with specific abstract comics, and jump to my final point, which is that the same structure underlies the appreciation of many, if not all, sufficiently visually complex representational comics. Let me show you two examples from the work of Steve Ditko, each of which, in its own way, can be seen to transcend the simple illustration of a narrative in favor of a more abstract formal functioning. On one hand we have a sequential arrangement of forms in the “Wraith-taint” in Rom, issue 59, by Steve Ditko, which is largely based on the transformation of a single shape from panel to panel, therefore echoing the time-based sequential arrangements, both the illustrations of scientific processes and Trondheim’s metamorphic shapes in “Bleu”:

On the other hand, we have the more complex arrangements in these two pages from Amazing Spider-Man 23, the formal functioning of which is not so much a matter of sequential growth, but results largely from the interaction of shapes across the surfaces of the layouts, emphasizing panel-to-panel formal conflict, the clashing forces of differentiation:

In ways which could be detailed at length, but which I only have the time to suggest here, these two pages reveal as nakedly as possible the morphogenetic field of comics, the simple pre-existence of a homogenous conceptual grid and its presupposed vectors of forces–and the potential for such a vector field, through differentiation and symmetry breaking, to provide rich and unexpected sequential art experiences. This effect yields perhaps the highest kind of aesthetic satisfaction in comics, and it does so by largely bypassing any logic of literary illustration. Rather, it turns itself into an abstract model of system-formation, laying visible a complexity that transcends simple narrativity. Abstract comics have learned this lesson and done away with that narrativity altogether, but they could do so only by finding examples to follow in the work of masters such as Ditko.